- This video gives an introduction to the concept of 2-D and 3-D motion. When an object is free to move in a plane, it is called 2-D motion or motion in two dimensions. Two axes are required to describe such type of motion. When an object is free to move in a free space, it is called 3-D motion or motion in three Dimensions. It requires three axes to define such motion.
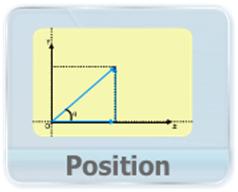
- This video explains the method of determining position in 2-D and 3-D motion according to the coordinate system of geometry in unit vector notation and magnitude-angle vector notation.
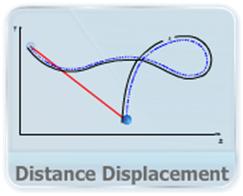
- This video explains the concept of distance and displacement and the method of calculating it for 2-D and 3-D motion in coordinate and vector notations.
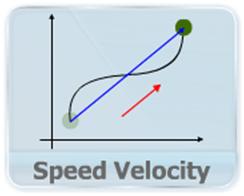
- This video explains the magnitude and direction average velocity, speed and instantaneous velocity for 2-D and 3-D motion. Average velocity is defined as the vector sum of average velocities along individual axes.
- This video explains the concept of acceleration in 2-D and 3-D motion as the vector sum of acceleration along individual axes. It also explains the concept of constant and varying acceleration; and the case of non-zero acceleration even if magnitude of velocity doesn’t change.
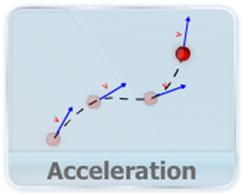
- This video explains the dependence of the physical quantities of 2-D and 3-D motion in constant acceleration upon the relative quantities in 1-D motion along with equations and graphical representation. Each quantity can be calculated for individual axes first, and then later, be combined as a vector sum to get the respective quantities for 2-D and 3-D motion.

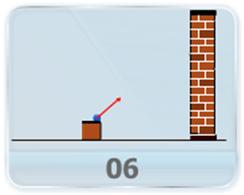
- This video demonstrate an example of 2-D motion called Projectile motion; along with kinematics equation and give introduction of its key terms and physical quantities like horizontal range, maximum height and angle of projection.
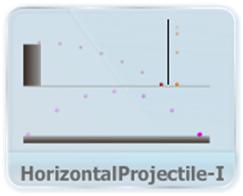
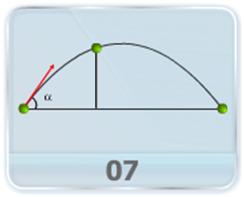
- This video shows the method of calculating the key physical quantities of projectile motion like maximum height, time of flight and range, by applying the kinematics equations along individual axes.
.jpeg)
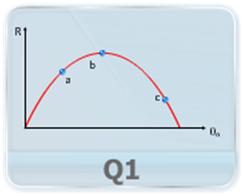
- Given figure shows the range R of the ball versus its launch angle for horizontal projectiles. Arrange the three lettered points on the plot in decreasing order according to (a) the total flight time of the ball and (b) the ball&#circular-motion-video-lectures-for-iit-jee-physics39;s speed at maximum height.
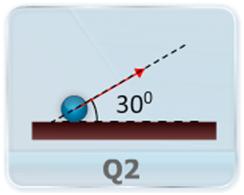
- A ball is thrown at an angle with a given initial speed. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point. (b) the maximum height reached. (c) the horizontal range of the ball. (d) the time for which the ball is in the air. (e) other angle of projection to attain the same range. (f) velocity and position of ball at t = 2 sec.
- A projectile is projected with a given initial velocity (in vector form) in a plane. Find (a) Horizontal range? (b) Time after which its inclination with the horizontal changes to some other angle?
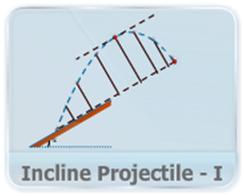
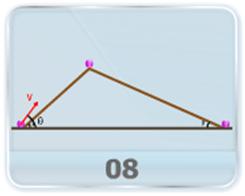
- This video explains the concept of projectile motion on an inclined plane which makes an angle with horizontal and shows a way to derive the key physical quantities like range and time of flight for the projection motion on an inclined plane.
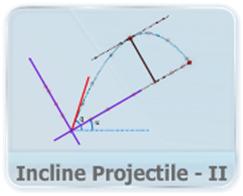
- This video shows an easier way to derive the key physical quantities for the projectile motion on an inclined plane using the shift of axes and resolving the components along these new axes.
- A particle is projected up an inclined plane of a given inclination b, at an elevation ‘a’ to the horizontal. Show that (a) tan a = cot b + 2tan b , if the particle strikes the plane at right angle. (b) tan a = 2tan b , if the particle strikes the plane horizontally.
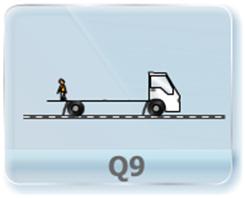
- This video explains the importance of frame of reference in describing the motion of an object. An object kept in a moving truck is stationary for an observer sitting in same truck and moving for an observer standing beside the road. It also explains the relative velocities in relation with choice of reference frame and the validity of equation of motion in different reference frames.
- This video shows the way to calculate the relative velocity with the shift in reference frame if the velocity in other frame of reference is given.
- A boat can travel at a given speed in still water. What will be the speed of boat while going downstream and upstream in a river with given slow speed.
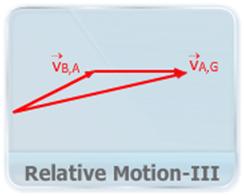
- This video explains the method to calculate relative motion in different frame of reference.
- A small body is dropped from a rising balloon by a person ‘B’ while another person ‘A’ stands on ground. Immediately after the body is released; what would A and B will feel about the direction of motion of the body with respect to them?
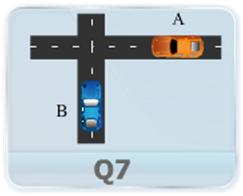
- Car A is traveling east at the constant speed of 10 m/s as shown in Figure. As car A crosses the intersection, car B starts from rest 50 m north of the intersection and moves south with a constant acceleration of 2 m/s2. Determine the position, velocity and acceleration of B relative to A, 5 sec after A crosses the intersection.
- A person driving a bike is standing on the road on a rainy day. If he starts to move with velocity v, In which direction will the rain appear to him if (a) Rain is falling vertically (b) Rain is falling at an angle away from him?

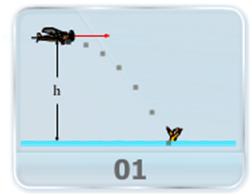
- A rescue plane files at some velocity and a constant height toward a point directly over a victim, where a rescue capsule is to land. The plane drops a rescue capsule while moving at constant velocity in level fight. While falling, the capsule remains under the plane. What should be the angle of the pilot&#circular-motion-video-lectures-for-iit-jee-physics39;s line of sight to the victim when the capsule is released and velocity of the capsule just before it lands?
- A ball is thrown from the top of a high building with a given speed at an angle above the horizontal. Find a) The time taken by the ball to reach the ground. b) The speed of the ball just before it touches the ground. c) How far is it from the tower horizontally when it lands?
- Two balls are thrown with the same initial velocity at complementary angles with the horizontal. Find the ratio and sum of the maximum heights attained by them.
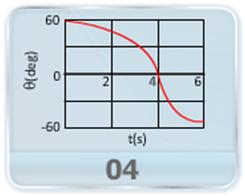
- Plotted is the graph of the angle that the instantaneous velocity of a ball in projectile motion makes with the horizontal as a function of time. Given is the total time of flight. (a) What is the magnitude of the launch velocity? (b) At what height above the launch does the ball land? (c) What is the direction of travel just as the ball lands?
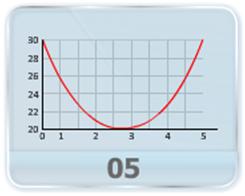
- A golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in figure, where t = 0 at the instant the ball is struck. Find the horizontal range and maximum height attained by the ball.
- A ball is thrown from a height of 1m above the ground with a given velocity of with an angle with the horizontal. There is a wall at a given distance from the point of projection such that the ball rebounds elastically from the wall. At what distance from the point of projection does the ball hit the ground?
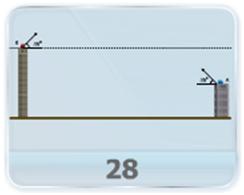
- A ball is thrown from a point on the ground at a given distance from the foot of a pole at an angle, which just touches the top of pole and strikes the ground at a distance on the other side of pole. Find the height of the pole.
- A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If the base angles of the triangle and angle of projection are given, Find the relationship between base angles and angle of projection?
- The ratio of the distance carried away by the water current downstream by a boat making same angle with downstream and upstream, while crossing a river is 2:1. The maximum ratio of speed of boat to the water current will be…..?

- A particle is projected at angle with the horizontal. Calculate the time instant when it is moving perpendicular to initial direction. Also calculate the velocity at this position.
- Car A and B move with different velocities; velocity of B is higher than A. Find (a) relative velocity of B w.r.t. A (b) relative velocity of A w.r.t. B (c) if initially there was some distance between them, what will be its value after a given time?
- Two roads intersect at right angle; one goes along x-axis and the other along y-axis. At any point of time, two cars A and B are moving along negative x and positive y direction respectively. Draw the direction of motion of Car A as seen from car B and vice-versa.
- A motorboat going downstream overcame a box at a point A. After time T, it turned back and after sometime passed the box at a given distance from the point A. Find the flow velocity assuming the duty of the engine to be constant.
- Flow velocity of a river and speed of a boat in still water is given. In which direction should the boat move, so that it crosses the river (a) in shortest time (b) along shortest path

- Two swimmers leave point A on one bank of river to reach point B lying right across on the other bank. One of them crosses the river along the straight line AB while the other swims at right angles to the stream and then walks the distance that he has been carried away by the stream to get point B. What was his walking speed if both swimmers reached the destination simultaneously? Given are the stream velocity and the velocity of each swimmer with respect to water.
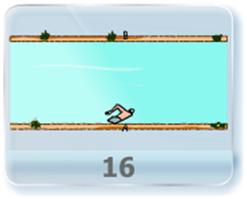
- A boat is moving directly away from a cannon on the shore with a speed v1. The cannon fires a shell with a speed v2 at an angle ‘a’ and the shell hits the boat. Then, which of the following is true. (a) the shell hits the boat when the time equals to (2v2 sin a)/g (b) the boat travels a distance (2v1v2 sin a)/g from its original position (c) the distance of the boat from the cannon at the instant the shell is fired is 2(v2 sin a)(v2 cos a - v1)/g (d) the distance of the boat from the cannon when the shell hits the boat is 2(v2 sin a)(v2 cos a )/g
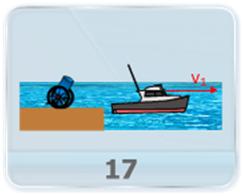
- Two shells are fired from cannon successively with same speed ‘u’ at angles of projection ‘a’ and ‘b’ respectively. If the time interval between the firing of shells is dt and they collide in mid-air after a time ‘t’ from the firing of the first shell. Then which of following is true. (a) T cosa = (t - dt) cosb(b) a > b(c) (t - dt) cosa = dt cosb(d) (u sina) t – ½ g dt2 = (u sinb) (t - dt) – ½ g (t - dt)2
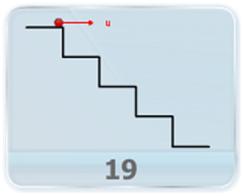
- A ball rolls off the top of a staircase with a horizontal velocity u m/s. If the steps are h meters high and b meters wide, which stair from the top will the ball hit?
- A stone is projected from the point on the ground in such a direction so as to hit a bird on the top of a telegraph post of given height and then attain the maximum height of 3/2th of the height of the post above the ground. If at the instant of projection, the bird were to fly away horizontally with uniform speed, find the ratio between horizontal velocities of the bird and stone if the stone still hits the bird while descending.
- Two parallel straight lines are inclined to the horizontal at an angle a. A particle is projected from a point mid way between them so as to graze one of the lines and strike the other at the right angle. show that if q is the angle between the direction of projection and either of the lines, then tan q = ( 2 - 1) cot a.
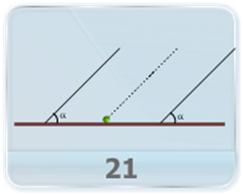
- Two particles move with different but constant velocities. At the initial moment their position vectors are given. How must these four vectors be interrelated for the particles to collide?
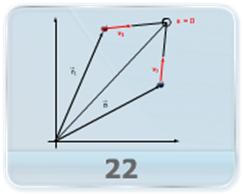
- On a frictionless horizontal surface, assumed to be the x-y plane, a small trolley A is moving along a straight line parallel to the y axis with a constant velocity. At a particular instant, when the line OA makes a certain angle with the x axis, a ball is thrown along the surface from the origin O. Its velocity makes a known angle with the x axis and it hits the trolley. If the motion of the ball is observed from the frame of the trolley, calculate the angle made by the velocity vector of the ball with the x axis in this frame. Also, find the speed of the ball with respect to the surface.
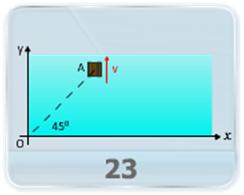
- Two particles start moving simultaneously with constant velocities u1 and u2 as shown in figure. First particle starts from N along NO and second starts from O along OM. Find the shortest distance between them during their motion.
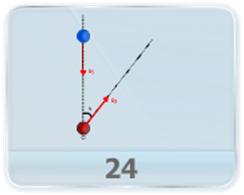
- Two particle start simultaneously from the same point and move along two straight lines making an angle ‘a’; one with uniform velocity and other with a uniform acceleration. Find the time at which the relative velocity is least and its value.
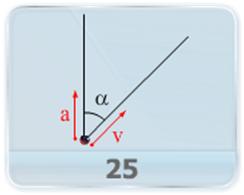
- What will the path of a projectile be as seen by an observer on another projectile?
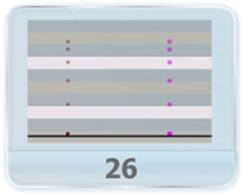
- Two particles A and B are projected simultaneously from top of two high towers at a distance apart with same initial velocity; one horizontally and other at angle to horizontal, towards each other. If they collide in mid-air after a while, find the distance between the towers.
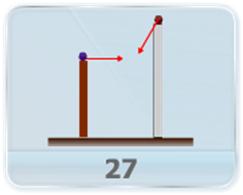
- Two particles A and B are projected simultaneously from two high rise buildings at a distance apart with different initial velocity at same angle of projection towards each other. Find minimum distance between these two particles at any point of time.
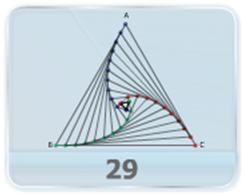
- Three particles A, B and C are situated at the vertices of an equilateral triangle ABC initially. Each of the particles moves with a given constant speed. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
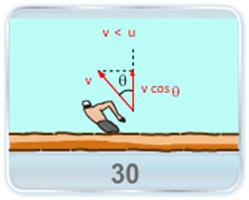
- A swimmer swims with velocity v in still water which is less than the velocity u of the river. Show that the swimmer must swim at an angle of cos-1 (v/u) with upstream in order to cross the river along the shortest possible path.
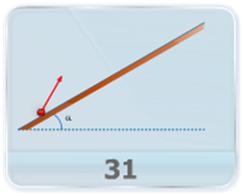
- Find maximum value of range for a projectile on an inclined plane which makes a given angle with horizontal.
- For a horizontal projectile with a known initial velocity; what can be the maximum height reached for a given horizontal distance?
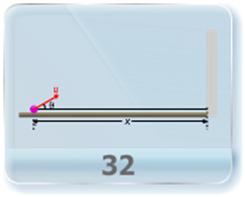
- A stone is being thrown at a given speed from the top of a high building. Find out how far from the foot of the building can the stone be thrown?
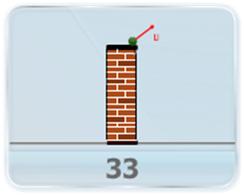







.jpeg)














































